|
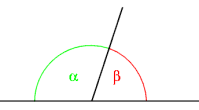
ÁNGULOSÁngulos adyacentesÁngulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.[1] [2] [3] 
Otros autores denominan ángulos adyacentes a los ángulos consecutivos.
En la literatura del tema es posible también encontrar casos donde se denomina como adyacentes a cualquier par de ángulos que compartan el vértice y un lado, aunque no sean suplementarios (es decir, se llaman adyacentes a los ángulos que en otros textos se denominan consecutivos),[4] [5] quizás debido a la influencia del inglés en donde adjacent angles tiene este significado. Por ello es importante al abordar un texto sobre el tema, tener presente cual es la convención usada. En este artículo se efectúa la distinción, considerando únicamente el caso en que los lados no comunes formen una línea recta, reservando el artículo ángulos consecutivos para la otra acepción. Propiedades
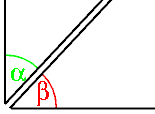
Ángulos complementariosLos ángulos complementarios son aquellos ángulos cuyas medidas suman 90º (grados sexagesimales). Si dos ángulos complementarios son consecutivos, los lados no comunes de los dos forman un ángulo recto. Así, para obtener el ángulo complementario de α, teniendo α una amplitud de 70°, se restará α de 90°:
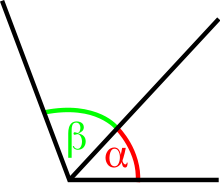
Sabiendo esto, dichos ángulos formarán siempre un triángulo rectángulo puesto que los ángulos en un triángulo rectángulo son uno de 90º y los otros dos deben sumar 90 con el del cateto adyacente y se multiplica por la hipotenusa (180º(grados totales de un triángulo)-90º=90º). Por tanto, el seno de α es igual al coseno de β y el seno de β igual al coseno de α puesto que pertenecen al mismo triángulo rectángulo. La diagonal de un rectángulo también configura ángulos complementarios. Ángulos consecutivos Los ángulos consecutivos son aquellos que poseen un mismo vértice y tienen un lado común. Así, dados varios ángulos, serán consecutivos cuando cada uno de ellos esté ordenado de forma que comparta un lado con ángulo siguiente y todos tengan el mismo vértice. Son ángulos consecutivos los conjugados y los adyacentes. Ángulos opuestos por el vértice Dos ángulos opuestos por el vértice son los ángulos opuestos
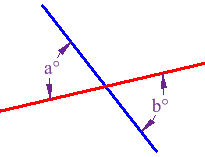
ÁNGULOS OPUESTOS POR EL VÉRTICE
Dadas dos rectas que se cortan, dos ángulos son opuestos por el vértice si tienen como vértice el punto de corte entre las rectas y los lados de uno son rayos opuestos de los lados del otro.
|
|