Concepto de fracción

CONCEPTO DE FRACCIONES

El concepto matemático de fracción corresponde a la idea intuitiva de dividir una totalidad en partes iguales, como cuando hablamos, por ejemplo, de un cuarto de hora, de la mitad de un pastel, o de las dos terceras partes de un depósito de gasolina. Tres cuartos de hora no son, evidentemente, la misma cosa que las tres cuartas partes de un pastel, pero se “calculan” de la misma manera: dividiendo la totalidad (una hora, o el pastel) en cuatro partes iguales y tomando luego tres de esas partes. Por esta razón, en ambos casos, se habla de dividir dicha unidad (una hora, un pastel, etc.) en 4 partes iguales y tomar luego 3 de dichas partes.

Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.

La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.

TÉRMINOS DE UNA FRACCIÓN

a	Numerador
—	-
b	Denominador

El Numerador indica el número de partes iguales que se han tomado o considerado de un entero. El Denominador indica el número de partes iguales en que se ha dividido un entero.

Por ejemplo, la fracción 3 / 4 (se lee tres cuartos) tiene como numerador al 3 y como denominador al 4. El 3 significa que se han considerado 3 partes de un total de 4 partes en que se dividió el entero o el todo.

La fracción 1 / 7 (se lee un séptimo) tiene como numerador al 1 y como denominador al 7. El numerador indica que se ha considerado 1 parte de un total de 7 (el denominador indica que el entero se dividió en 7 partes iguales).

Ejemplos:

Hay 8 partes de las cuales se han pintado 5, por lo tanto, la fracción que representa matemáticamente este dibujo es 5 / 8 (se lee cinco octavos).

Hay 3 partes pintadas de un total de 5. Esto se representa como 3 / 5 (se lee tres quintos)

Debes tener presente que existen distintas posibilidades para representar gráficamente una fracción, es decir, se puede representar con distintos dibujos; lo importante es tener siempre presente el concepto de fracción.

Por ejemplo, la fracción 5 / 8, que ya vimos arriba, está representada a continuación de otras dos formas distintas:

Hay 5 partes pintadas de un total de 8 partes. Esto se representa como 5 / 8 (se lee cinco octavos)

Hay 1 parte pintada de un total de 2 partes. Esto se representa como 1 / 2 (se lee un medio)

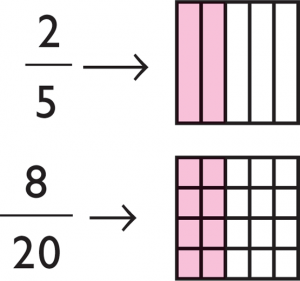
Concepto de fracciones

$Concepto de fracciones$ Las fracciones son también llamados números racionales o quebrados, y representan porciones de un todo. Significa roto o quebrado, según su etimología latina.

Si consideramos por ejemplo, una torta o una hoja de papel, y las dividimos en partes iguales, cada parte representará una porción del todo. Si la dividimos en cinco partes, cada una de ellas será la 1/5 parte de ese todo, que será de 5/5.

Los números que componen una fracción se representan separados por una barra horizontal. El número que se coloca debajo de la barra, se llama denominador, y es el que indica en cuantas partes se dividió la unidad. El que va por encima de la barra, se llama numerador, y expresa la cantidad de partes que se toman o descartan.

Cuando el denominador es 2, la unidad fraccionaria se denomina medio. Así ½, se lee un medio; si el denominador es tres, se lee, tercio, y así hasta el décimo. En denominadores superiores al número10, se agrega “avo” al nombre del número (onceavo, doceavo…)

Los números fracciones que poseen idénticos denominadores, se llaman números fraccionarios homogéneos. Si dos fracciones poseen el mismo denominador positivo la fracción mayor, es la que tiene mayor numerador. Si dos fracciones tienen igual numerador, la mayor es la que posee un denominador de número menor.

Los números fraccionarios decimales son los que tienen como denominador, la unidad seguida de ceros.

Dos fracciones iguales se denominan equivalentes. En la ilustración se muestran dos fracciones iguales o equivalentes, ya que si se las reduce, dividiendo por el mismo número el numerador y el denominador (en esye caso 4) de la fracción de números más grandes (8/20) nos da dos fracciones idénticas. Las fracciones pueden ser susceptibles de operaciones matemáticas de comparación, suma, resta, multiplicación y división.

Concepto de etimología

El vocablo etimología, deriva del latín “etymologĭa”, y a su vez del griego; siendo “étymos”, “lo verdadero” y “logos”, “el estudio”. De acuerdo a ello, podemos definir a la etimología, como la disciplina cuyo objeto de estudio es el verdadero o auténtico origen de las palabras y su evolución, atendiendo a sus circunstancias; tanto en su forma como en su significado, al ser introducidas a otro idioma.

La mayoría de las palabras del idioma castellano, por ser una lengua romance, tienen su origen en el latín vulgar, introducido por los romanos con la conquista del territorio español, hacia el año 200 antes de la era cristiana, aunque pueden reconocerse la influencia de otras lenguas, en especial el árabe, al sufrir España la invasión de los moros. Entre las palabras de este último origen podemos mencionar: alcohol, alhaja, ojala o ajedrez. Del francés provienen por ejemplo las palabras garaje, hotel o souvenir; del italiano, máscara o pizarra; del inglés se adoptaron vocablos como “líder”; y en América latina, derivadas de las culturas aborígenes, nos han llegado como legados chocolate, elote y cacique.

La etimología es muy útil para lograr una correcta ortografía y conocer el real significado del vocabulario que empleamos, al que enriquecemos, y descubrimos en sus comienzos, y observamos las transformaciones que ha sufrido a lo largo del tiempo, donde muchas palabras son dejadas de usar, reemplazadas por otras, modificadas, o se incorporan otras nuevas, producto del contacto con otras culturas; más aún en tiempos actuales, gracias al proceso de globalización. Por ejemplo la palabra football, derivada del inglés, fue castellanizada como fútbol.

Concepto de positivo

La palabra positivo, deriva en su etimología del latín “positivus” que significa acorde a lo establecido por convención, que se supone bueno. En este sentido el Derecho Positivo en el ámbito jurídico designa el que ha sido convenido por los hombres y plasmado en leyes escritas modificables según lo exija el cambio de costumbres y la cultura valorativa de cada sociedad, a diferencia del Derecho Natural, no escrito, eterno e inmutable, reconocido por la conciencia, que para los iusnaturalistas debe insirar al Derecho Positivo

Se dice que alguien es positivo en su forma de actuar cuando ve lo conveniente, lo agradable, lo bueno de las cosas, que seguramente es lo que debiera ser establecido para vivir cada día mejor. Una actitud o una respuesta positiva suma, agrega y perfecciona. Por el contrario el negativo es el que resta, pone escollos e impide el progreso.

Un test de embarazo con resultado positivo anuncia la llegada de un bebé. Un examen médico positivo indica la presencia de la enfermedad que se quería diagnosticar y una evaluación escolar positiva significa que se aprobó. En todo los casos confirma la existencia (de una nueva vida, de una dolencia o de conocimientos, respectivamente).

En Matemática los números positivos son aquellos mayores que el número neutro cero.

La carga eléctrica positiva es una propiedad de la materia que hace que cuando se encuentra en un campo eléctrico, experimente la fuerza en igual sentido al del campo. Son positivos por ejemplo los polos de un generador que tienen la capacidad de atraer las cargas negativas y repeler las positivas.

Concepto de decimales

La palabra decimal puede referirse al sistema numérico, llamado también indo-arábigo, pues nació en la India y entró a Europa de la mano de la invasión árabe, que lo modificó. Sus cantidades se expresan sobre la base del número 10.

Se supone según estudios antropológicos, que el hombre siempre tendió a contar usando los diez dedos de sus manos, y ese habría sido el origen de este sistema, donde el uno representa a la unidad en sí misma, dos, una unidad y otra; tres, dos unidades y otra más, y así sucesivamente, agregando una unidad a la anterior. Al reunirse diez unidades se conforma una decena, diez decenas forman una centena, etcétera. Cuando se expresa un número cualquiera, por ejemplo, 48, se está diciendo 40 decenas, y 8 unidades.

Se llaman números decimales, a los que resultan de dividir aquellos fraccionarios donde el numerador es menor que el denominador, o que siendo mayor, no dé por resultado un número entero. Una fracción de estas características puede convertirse en número decimal simplemente dividiendo el numerador por el denominador, llamándose decimales los números que se hallan luego de la coma. Así ¾ nos da el siguiente número decimal: 0,25. Al leer este número se dice primero la parte entera (en este caso, cero) y luego la parte decimal veinticinco centésimas. Se trata de un número menor que la unidad. Si consideramos la fracción 5/4 nos da un número decimal mayor que la unidad: 1,25.

Si se mueve la coma decimal de derecha a izquierda, se hace diez veces menor, por cada lugar que se corra.

Se llaman unidades fraccionarias decimales, aquellas fracciones que tienen al número 1 como numerador y como denominador, la unidad seguida de ceros. Los números fraccionarios decimales son los que tienen por denominador, la unidad seguida de ceros y cualquier número como numerador.

Transformar decimal a fracción

OPERACIONES CON DECIMALES

Para poder tomar los exámenes

de este tema debes estar

registrado, si no lo estás,

[Registrate aquí]

Entrar a exámenes de:

En el siglo XVI d.C., los matemáticos europeos comenzaron a notar la facilidad con la cual se efectuaban los cálculos con números fraccionarios cuyos denominadores fueran potencias de 10. Por ejemplo:

Naturalmente, para sumar las fracciones anteriores basta con tomar 10.000 como denominador común y se obtiene

Este tipo de fracción se llama fracción decimal.

Un ingeniero y matemático holandés llamado Simón Stevin inventó en el S. XVI un método para hacer cálculos con fracciones decimales sin usar el denominador. Por ejemplo, escribía

	como
	como
	como

Al sumar estos números, obtenía

Aunque su método no llegó a usarse mucho, su idea fue tomada por un gran matemático escocés, Napier, quien desarrolló, a partir de la proposición de Stevin, otra manera de escribir las fracciones decimales.

Al principio, colocó una línea debajo de los dígitos del numerador, de esta manera:

Finalmente, ya en 1617, Napier propuso el uso de una coma o un punto para separar la parte entera de la parte decimal:

Esta última idea de Napier fue la que se adoptó definitivamente para escribir los que hoy se llaman números decimales.

Sabiendo que el origen de la escritura de los números decimales está vinculado a la necesidad de facilitar los cálculos con fracciones decimales, es bueno notar que luego se encontró la forma de expresar cualquier fracción como un número decimal.

La mayor facilidad para los cálculos radica en que sólo se efectúan las operaciones con números enteros y no ya con fracciones, pues al escribir, por ejemplo, tex2html_wrap_inline516 en la forma decimal, se obtiene (2,5)(0,03) y en realidad esta operación requiere sólo que se multipliquen los números enteros

y luego se le coloca la coma de manera que se obtengan 3 espacios ocupados a la derecha de la coma, y se escribe entonces

Es importante saber que, en los tiempos en que esta idea surgió, no existían, por supuesto, calculadoras que ayudaran a los científicos en la realización de cálculos complicados. En ciertas áreas, como en la astronomía, por ejemplo, los cálculos complicados requerían de mucha precisión.

Los números decimales se usaron finalmente, no sólo para representar fracciones decimales, sino cualquier fracción en general.

Por ejemplo, sabemos que tex2html_wrap_inline520 , lo cual se puede obtener escribiendo como fracción decimal, de la siguiente manera:

se multiplican numerador y denominador por 5, en este caso, pues se sabe que y esa operación permitirá encontrar la fracción equivalente a que tiene denominador igual a 10:

Otra manera de obtener esto, es la siguiente:

La serie de operaciones mostradas equivale a la división , que se realiza multiplicando el dividendo por 10, por ser menor éste que el divisor:

El paso final de colocar la coma en el sitio correcto equivale a la multiplicación por , en este caso:

De esta manera, es posible encontrar la expresión decimal que corresponde a una fracción cualquiera.

Si la fracción es impropia, se realiza la división del numerador entre el denominador, de la manera usual, y se obtiene la expresión decimal de la fracción.

Por ejemplo:

Ocurre con algunas fracciones algo curioso: cuando se realiza la división del numerador entre el denominador, se obtienen cifras decimales que se repiten indefinidamente, como en el caso de .

al efectuar la división, en cada paso se obtiene resto igual a 2 y así, la expresión decimal en cuestión es:

Los puntos suspensivos indican que la sucesión de 6 ¡no tiene fin!

Esta expresión se llama expresión decimal periódica y también se escribe así:

El número que se repite, en este caso, el 6, es llamado el período de la expresión decimal.

En algunos casos, el período tiene más de una cifra, por ejemplo:

Ciertamente, es interesante la existencia de estas expresiones decimales para números cuya expresión fraccionaria es tan sencilla como .

El período de la expresión decimal periódica de es 142857.

Hay casos en los que la expresión decimal periódica tiene esta forma:

en este ejemplo, el período comienza después de las cifras decimales: 01. Estas dos cifras constituyen el anteperíodo de la expresión decimal.

Como se ha visto, toda fracción se puede expresar como número decimal, bien sea con una cantidad finita, limitada, de cifras decimales, o bien con una cierta cantidad de cifras decimales que se repiten de manera periódica infinitas veces.

Se verá a continuación cómo se logra expresar como fracción, un número que está escrito en su expresión decimal, bien sea con un número finito de cifras decimales, o por un período.

Podría el lector preguntarse si existe la posibilidad de que un número, en su expresión decimal, tenga una cantidad infinita de cifras decimales no periódicas, es decir, que las cifras no se repitan con ningún patrón y que sea ilimitado su número.

La respuesta es que tales números sí existen y son llamados irracionales.

Es muy importante saber reconocer, entre dos números decimales, cuál es mayor.

Por ejemplo, entre 5,9 y 6,1, sabemos reconocer a 6,1 como el mayor de los dos, porque la parte entera de 6,1 es 6, que es mayor que 5, y no importa que la parte decimal de 6,1 sea 1, mientras que la de 5,9 es 9, que es mayor que 1. Así,

En el lenguaje común se expresa la idea de proporción con cierta frecuencia.

Fracción Generatriz.

Si bien algunas expresiones decimales, como 0,25, pueden expresarse como fracción fácilmente, simplemente escribiendo (en el denominador se escribe porque hay dos cifras decimales en la expresión decimal 0,25), hay otras que a primera vista parecen tener dificultades mayores, como por ejemplo:

Realmente no es tan difícil llevar esta expresión decimal a su expresión fraccionaria, llamada "la fracción generatriz'' del número decimal en cuestión.

La manera de encontrar esta fracción generatriz es la siguiente:

Se multiplica la expresión decimal periódica tex2html_wrap_inline552

por

, escogiéndose la potencia 3 porque el período tiene 3 cifras. Si se llama x a la fracción generatriz, se tiene que

ya que

Restando x a 1.000x se obtiene

Pero, por otro lado,

por lo tanto,

Simplificando, se obtiene

como la fracción generatriz de tex2html_wrap_inline552

Las expresiones decimales periódicas con anteperíodo, como por ejemplo:

también pueden llevarse a su forma fraccionaria. Para encontrar la fracción generatriz de esta expresión decimal, se comienza por multiplicarla por 10:

De esta manera, se obtiene una expresión decimal periódica cuyo período comienza después de la coma, es decir, se elimina el anteperíodo.

De nuevo, se llama x a la fracción generatriz, que, en definitiva, es el mismo número

Así,

ahora,

restando ahora 1000x-10x se obtiene

es decir, 1000x-10x=2982, luego 990x=2982 y

Si has acertado en todas tus respuestas, ¡felicitaciones! has hecho un buen progreso en tu camino a través del mundo de los números. Si has cometido algunos errores, asegúrate de comprender la causa de los mismos, para no cometerlos nuevamente en el futuro.

REPASO DE DECIMALES

Para poder tomar los exámenes

de este tema debes estar

registrado, si no lo estás,

[Registrate aquí]

Entrar a exámenes de:

Contenido Revisado

REPASO DE DECIMALES

Objetivos:

Escribir un decimal como una fracción.
Sumar y restar decimales.
Escribir una fracción como un decimal.
Convertir decimales en porciento y de porciento a decimales.
Convertir fracciones en porciento y de porciento a fracciones.

Explicación

Cada número decimal tiene dos partes separadas por el punto decimal. La parte izquierda del punto decimal es la parte del número entero , y la parte derecha del punto decimal contiene la parte fraccionaria. Por ejemplo, el número 33.45

33 es la parte entera, el número entero.
45 es la parte fraccionaria.

Cada dígito en un número entero tiene su valor posicional. Estos son : unidades,decenas, unidad de millar, decena de millar, centena de millar, etc.
.
Cada dígito de la parte derecha del punto decimal ocupa una posición con un valor posicional fraccionario. Para leer la parte fraccionaria de un número decimal, notamos la posición donde el último dígito aparece. El valor posicional nos indica si estamos utilizando décimas, centésimas o milésimas, etc. Los dígitos indican cuántas décimas, centésimas o milésimas tenemos.

Ejemplo:

Convertir los decimales a palabras y a fracción.

Forma Decimal	Forma en palabras	Forma Fraccionaria Simplificada
0.5	5 décimas	5 ÷ 5 = 1 10 5 2
0.23	23 centésimas	23 100
0.133	133 milésimas	133 1000
43.56	43 y 56 centésimas	43 56 = 4356÷ 4 = 1089 100 100 4 25

Ejemplos:

Escribir 0.014 como una fracción simplificada

Para simplificar una fracción, se divide el numerador y denominador por un número que los divide en común.

Solución:

0.014 = 14 ÷ 2 = 7
1000 2 500

Como miramos la parte fraccionaria, vemos que es .014 La posición indica que es 14 milésimas. Por lo tanto, la fracción es 14/1000.

Escribir 0.94 como una fracción simplificada.

Solución:

0.94 = 94 ÷ 2 = 47
100 2 50

Ejemplo: Escribir 24 como número decimal.
1000

Note que el 0 es a veces posicionado en la parte izquierda del punto decimal donde no hay parte entera del número. Esto es hecho simplemente para llamar la atención a la localización del punto decimal y es la notación internacional aceptada.

24 = 0.024
1000

Ejemplo: Escriba 3.55 en palabras.

Solución: 3.55 significa 3 y 55 centésimas

Note que al leer un número decimal decimos "y" cuando alcanzamos el punto decimal. Esto señala que hemos terminado con la parte del número entero y nos estamos moviendo para leer la parte fraccionaria.

Ejemplo: Escriba 12.433 en palabras.

Solución: 12.433 significa 12 y 433 milésimas

Ejemplo: Escriba 23.5 en palabras.

Solución: 23.5 significa 23 y 5 décimas.

Redondear Números Decimales

A veces es necesario redondear a un lugar en particular. Debemos mirar el número que está a la derecha de lo que queremos redondear primero. Si deseamos redondear un número decimal a la décima, debemos fijarnos del núkmero a la centésima. Si deseamos redondear a la centésima, debemos mirar al número a la milésima, etc.

Pasos para redondear números:

1. Fíjate en el dígito que está en la posición inmediatamente a la derecha de la posición de donde queremos redondear el número.
2. Si el dígito en esta posición es menor que 5, deja el dígito a redondear tal como está.
3. Si el dígito en la posición a la derecha es igual o mayor que 5, suma 1 al dígito en la posición del redondeo.
4. Eliminar todos los dígitos a la derecha del lugar a redondear.

Ejemplo: Redondear 23.45 a la décima.

Solución: El dígito en el lugar de la centésima es 8, y 8 > 5, así que

23.45 es redondeado a 23.5

Suma de Decimales:

En la suma de números decimales, tenemos que alinear los puntos decimales y añadir dígitos de 0 en la columna que falta. Por ejemplo:

a. 3.45 + .8

                                                3.45
                                          +    0.80
                                                4.25

Se le añadieron los ceros donde faltaba, pero siempre recordando que el punto decimal debe estar alineado.

b. 2.15 + 78.123

                                            78.123
                                        + 02.150
                                            80.273

c. 0.23 + .002135

                                         0 .002135
                                    +   0.230000
                                         0.232135

Resta de Decimales

En la resta de decimales, es similar a la adición.

Ejemplo a. 0.4 - 0.2

                                        0.4
                                     - 0.2
                                        0.2

Ejemplo b. 245.67 - 3.15

                                    245.67
                                 - 003.15
                                    242.52

Ejercicios:

A) Convertir los decimales a palabras.

1) 0.49

2) 0.6

3) 1.323

4) 41.93

5) 1.19

B) Convertir las palabras a decimales.

1) 42 centésimas

2) 3 décimas

3) 22 y 19 centésimas

4) 237 milésimas

5) 1 y 47 centésimas

C) Convertir decimal en fracción o fracción a decimal.

1) 3
10

2) .125

3) 43
100

4) .381

Soluciones:

A)
1) 49 centésimas

2) 6 décimas

3) 1 y 323 milésimas

4) 41 y 93 centésimas

5) 1 y 19 centésimas

B)
1) 0.42

2) 0.3

3) 22.19

4) .237

5) 1.47

C)
1) .3

2) 125
100

3) .43

4) 381
1000

5) 23.100

6) 26 19
100

D)
1) 14.98 = 15

2) 24.956 = 24.96

3) 14.9213 = 14.9

4) 9.54319876 = 9.54

5) 14.986234954 = 14.986

E)
1) 23.08 + .04

             23.08
          + 00.04
             23.12

2) 43.5 + 1.5678

             43.5
          + 01.5678
             45.0678

3) 3.4 + 500.96

             003.40
           +500.96
             504.36

4) .04 + 312.55

              000.04
           +312.55
              312.59

F)
1) 43.689 - 2.15

             43.689
           -02.150
             41.539

2) 513.25 - .99

             513.25
           -000.99
             512.26

3) 43.92 - 1.53

             43.92
           -01.53
             42.39

4) 129.33 - 65.13

             129.33
           -065.13
               64.20

Fórmulas para operar fracciones

Suma de Fracciones con el mismo denominador

$frac{a}{c} + frac{b}{c} = frac{a + b}{c}$

Suma de Fracciones de diferentes denominadores

$frac{a}{c} + frac{b}{d} = frac{ad + bc}{cd}$

Resta de Fracciones con el mismo denominador

$frac{a}{c} - frac{b}{c} = frac{a - b}{c}$

Resta de Fracciones de diferentes denominadores

$frac{a}{c} - frac{b}{d} = frac{ad - bc}{cd}$

Multiplicación de Fracciones

$frac{a}{c} * frac{b}{d} = frac{ab}{cd}$

División de Fracciones

$frac{a}{c} / frac{b}{d} = frac{a}{c} * frac{d}{b} = frac{ad}{cb}$

Operaciones con fracciones

Vamos a suponer que tenemos 4 numeros representados por las letras a,b,c,d.

Sumas y Restas

$frac{a}{b} + frac{c}{d}$

Para la suma, tenemos los casos siguientes:

1. Denominadores iguales

$frac{7}{4} + frac{11}{4}$

Cuando tenemos los dos denominadores con el mismo valor, el resultado se obtiene copiando el denominador y sumando los numeradores.

Por ejemplo,

$frac{7}{4} + frac{11}{4} = frac{7 + 11}{4} = frac{18}{4}$ $frac{17}{3} - frac{7}{3} = frac{17 - 7}{3} = frac{10}{3}$

2. Denominadores diferentes

$frac{7}{24} + frac{10}{32}= frac{7}{2^3*3}+frac{10}{2^5}=frac{7*3+10*2^2}{2^3}=frac{21+40}{8}=frac{61}{8}$

Si los denominadores son diferentes, entonces se utiliza el método del mínimo común múltiplo para encontrar el denominador de la fracción resultante.

3. Fraccion de un número

Se debe de multiplicar ese número por el númerador y se divide el resultado por el denominador.

$frac{2}{5} * 3 = frac{6}{5}$

4. Producto de dos Fracciones

Se deben multiplicar los numeradores entre sí y los denominadores entre sí.

$frac{1}{3} * frac{1}{6} = frac{1}{18}$

5. División de Fracciones

En la división de fracciones, siempre se cambia a multiplicación y la segunda fracción cambia a su recíproco.

$frac{3}{5} / frac{4}{3} = frac{3}{5} * frac{3}{4} = frac{9}{20}$

Simplificación de Fracciones

Las fracciones se pueden reducir o simplificar; y el resultado sería una fracción equivalente. Por ejemplo, $frac{3}{6}$ se puede simplificar dividiendo por un numero que sea divisible por 3 y 6; en este caso, el 3.